Dreieckshöhen- und ihr Schnittpunkt
Links:
Matheprofi:
Beispiel einer Berechnung der Koordinaten des Höhenschnittpunkts anhand der Koordinaten der Dreieckspunkte - jedoch keine allgemeine Formel
Beispiel einer Berechnung der Koordinaten des Höhenschnittpunkts anhand der Koordinaten der Dreieckspunkte - jedoch keine allgemeine Formel
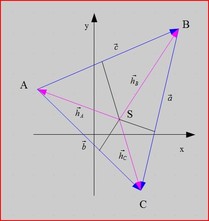
Die Höhen eines Dreiecks ABC schneiden einander in einem Punkt S(Sx;Sy).
Die Koordinaten Sx und Sy errechnen sich unter Heranziehung der Koordinaten der Dreieckspunkte A(Ax;Ay), B(Bx;By) und C(Cx;Cy) wie folgt:
Sx = ((By-Ay)*Cy^2 + ((Bx-Ax)*Cx - By^2 + Ay^2)*Cy + (Ax*Ay - Bx*By)*Cx + Ay*By^2 + (Ax*Bx - Ay^2)*By - Ax*Ay*Bx) / ((Bx-Ax)*Cy + (Ay-By)*Cx + Ax*By - Ay*Bx)
und
Sy = -(((By-Ay)*Cx - Bx*By + Ax*Ay)*Cy + (Bx-Ax)*Cx^2 + (Ax^2 - Bx^2)*Cx + (Ay*Bx - Ax*Ay)*By + Ax*Bx^2 - Ax^2*Bx) / ((Bx-Ax)*Cy + (Ay-By)*Cx + Ax*By - Ay*Bx)
[Bei der Gleichung nach “Sy = ” das vorangestellte Minuszeichen nicht übersehen!]
Herleitung der Gleichungen -
Portable Document Format [209 KB]:
Dreieckshoehen.pdf
Herleitung der Gleichungen -
OpenDocument Text [418 KB]:
Dreieckshoehen.odt
Berechnung der Schnittpunktskoordinaten der Dreieckshöhen -
Microsoft Excel Tabelle [8 KB]:
Dreieckshoehen.xls